The parabola has horizontal tangent lines at the point(s) (xy)/xy2 The parabola has calculous Find the area of the region bounded by the parabola y = 4x^2, the tangent line to this parabola at (4, 64), and the xaxis math Consider the parabola y = 7x x20 x a According to the arc length formula, L(a) = Z a 0 p 1 y0(x)2 dx = Z a 0 p 1 (2x)2 dx Replacing 2x by x, we may write L(a) = 1 2 Z 2a 0 p 1 x2 dx Thus theFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience

Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic
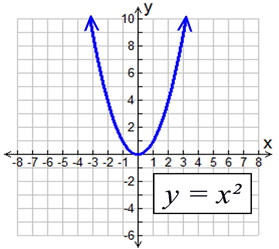
Parabola of y x 2
Parabola of y x 2-The equation of parabola can be expressed in two different ways, such as the standard form and the vertex form The standard form of parabola equation is expressed as follows f (x) = y= ax2 bx c The orientation of the parabola graph is determined using the "a" value If the value of a is greater than 0 (a>0), then the parabola graphParabola Calculator This calculator will find either the equation of the parabola from the given parameters or the axis of symmetry, eccentricity, latus rectum, length of the latus rectum, focus, vertex, directrix, focal parameter, xintercepts, yintercepts of the entered parabola To graph a parabola, visit the parabola grapher (choose the




Parabola Parent Function Mathbitsnotebook A1 Ccss Math
Parabola Opens Right Standard equation of a parabola that opens right and symmetric about xaxis with vertex at origin y 2 = 4ax Standard equation of a parabola that opens up and symmetric about xaxis with at vertex (h, k) (y k) 2 = 4a(x h) Graph of y 2 = 4axExplain why or why not 97 Write the equation of a parabola that opens up or down in standard form and the equation of a parabola that opens left or right in standard form Provide a sketch of the parabola for each one, label the vertex and axis ofSelect a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Substitute the x x value − 2 2 into f ( x) = √ − x f ( x) = x In this case, the point is ( − 2, ) ( 2, )
Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open downY = x 2 5x 3;Shifting parabolas The graph of y= (xk)²h is the resulting of shifting (or translating) the graph of y=x², k units to the right and h units up For example, y= (x3)²4 is the result of shifting y=x² 3 units to the right and 4 units up, which is the same as 4
Is the parabola x = y 2 x = y 2 a function?The Parabola Algebraic Definition of The Parabola Recall that the standard equation of the parabola is given by y = a (x h) 2 k If we are given the equation of a parabola y = ax 2 bx c we can complete the square to get the parabola in standard form Geometry of the Parabola We can define a parabola as followsFinding the focus of a parabola given its equation If you have the equation of a parabola in vertex form y = a ( x − h) 2 k, then the vertex is at ( h, k) and the focus is ( h, k 1 4 a) Notice that here we are working with a parabola with a vertical axis of symmetry, so the x coordinate of the focus is the same as the x coordinate of



Y X 2 2



Quadratics
Similarly, if we are given an equation of the form y 2 AyBxC=0, we complete the square on the y terms and rewrite in the form (yk) 2 =4p(xh)From this, we should be able to recognize the coordinates of the vertex and the focus as well as the equation of the directrix Given the Equation #color(red)(y=f(x)=4x^2# A Quadratic Equation takes the form #color(blue)(y=ax^2bxc# Graph of a quadratic function forms a Parabola The coefficient of the #color(red)(x^2# term (a) makes the parabola wider or narrow If the coefficient of the #color(red)(x^2,# term (a) is negative then the parabola opens down The term Vertex is used Graph y=3 (x2)^25 is a quadratic equation in vertex form y=a (xh)^2k, where h is the axis of symmetry and (h,k) is the vertex In order to graph a parabola, you need the vertex, the yintercept, xintercepts, and one or more additional points Vertex maximum or minimum point of the parabola



Quadratics



Parabola Parent Function Mathbitsnotebook A1 Ccss Math
The tangents to the parabola `y^2=4a x` at the vertex `V` and any point `P` meet at `Q` If `S` is the focus, then prove that `S PdotS Q ,` and `S V` asked in Parabola by TanujKumar ( 707k points) How do I show that the tangent to the parabola y=x^2 at a point (x0,y0) other than the vertex has xintercept at 1/2x0 closed Ask Question Asked 1 month ago Active 1 month ago Viewed 67 times 0 1 $\begingroup$ Closed This question does notAnswer (1 of 7) Yes, its axis of symmetry is the xaxis If you have a quadratic equation in two unknowns, Ax^2BxyCy^2DxEyF=0 you can tell if the curve it represents is a parabola or not by its discriminant B^24AC If the discriminant is 0, it's a parabola;



The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com



Practice Exam 1
Step 1 Solve for the vertex of the parabola The vertex of a parabola of the form {eq}y= x^2 bx c {/eq} is always given by {eq}\left (\dfrac {b} {2a},f (\dfrac {b} {2a})\right) {/eq} StepThe axis of symmetry will have the equation y = k Its form will be x = a( y – k) 2 h Example 1 Draw the graph of y = x 2 State which direction the parabola opens and determine its vertex, focus, directrix, and axis of symmetry The equation y = x 2 can be written as y = 1( x – 0) 2 0 so a = 1, h = 0, and k = 0The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y = x 2 3 Graph of y = x 2 3 The graph is shifted up 3 units from the graph of y = x 2, and the vertex is (0, 3)



An Exploration Of The Graph Of Y Ax 2 Font



Algebra Parabola Transformations Of Y X 2 Graphs Match Up 1 Teaching Resources
Since the given equation involves x 2 {{x}^{2}} x 2, the axis of the parabola is the yaxis Equation of directrix, y = a ie = 4 Length of latus rectum = 4a = 16 Illustration 6 If the parabola y 2 = 4x and x 2 = 32y intersect at (16, 8) at an angle θ, then find the value of θ Solution The slope of the tangent to y 2 = 4x at (16, 8) isThe children are transformations of the parent Some functions will shift upward or downward, open wider or more narrow, boldly rotate 180 degrees, or a combination of the above Learn why a parabola opens wider, opens more narrow, orParabolas A quadratic function is a function that can be written in the form f ( x) = a x 2 b x c where a, b, and c are real numbers and a ≠ 0 This form is called the standard form of a quadratic function The graph of the quadratic function is a Ushaped curve is called a parabola The graph of the equation y = x 2, shown below, is a



Solution How To Graph A Parabola Using Y X2 2x 8



Quadratics Graphing Parabolas Sparknotes
PARABOLAS TRANSLATIONS AND APPLICATIONS QUADRATIC RELATION A quadratic relation in two variables is a relation that can be written in the form y=ax^2bxc or x=ay^2byc where a, b, and c are real numbers, and a!=0 The graphs of quadratic relations are called parabolas The simplest quadratic relation of the form y=ax^2bxc is y=x^2, with a=1, b=0, and c=0, so thisWhat is the following parabola's axis of symmetry of $$ y =x^2 2x 3 $$ Answer Since this equation is in standard form, use the formula for standard form equation $$ x = \frac{ b}{ 2a} $$ Answer the axis of symmetry is the line $$ x = 1 $$ Problem 7 What is the following parabolaKey Takeaways The graph of any quadratic equation y = a x 2 b x c, where a, b, and c are real numbers and a ≠ 0, is called a parabola;



Exploration Of Parabolas



1
Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axis The original question from Anuja asked how to draw y 2 = x − 4 In this case, we don't have a simple y with an x 2 term like all of the above examples Now we have a situation where the parabola is rotated Let's go through the steps, starting with a basic rotated parabola Example 6 y 2 = x The curve y 2 = x represents a parabola rotatedThe Arc Length of a Parabola Let us calculate the length of the parabolic arc y = x2;
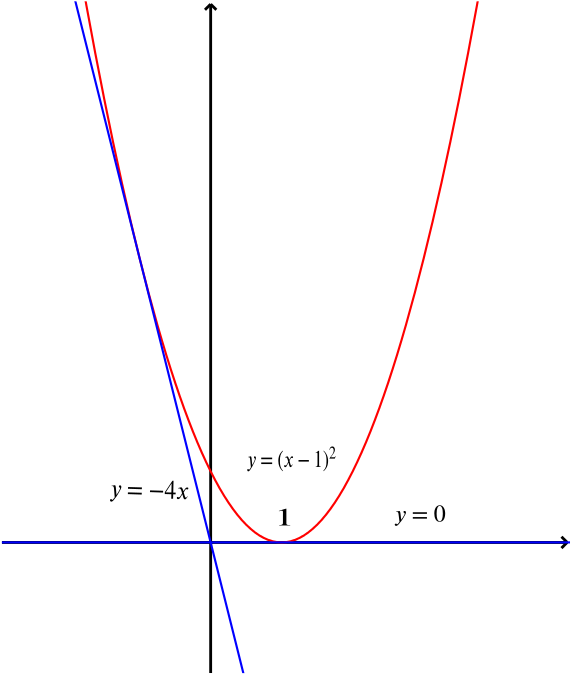



Solution When Does Y Kx Intersect The Parabola Y X 1 2 Quadratics Underground Mathematics
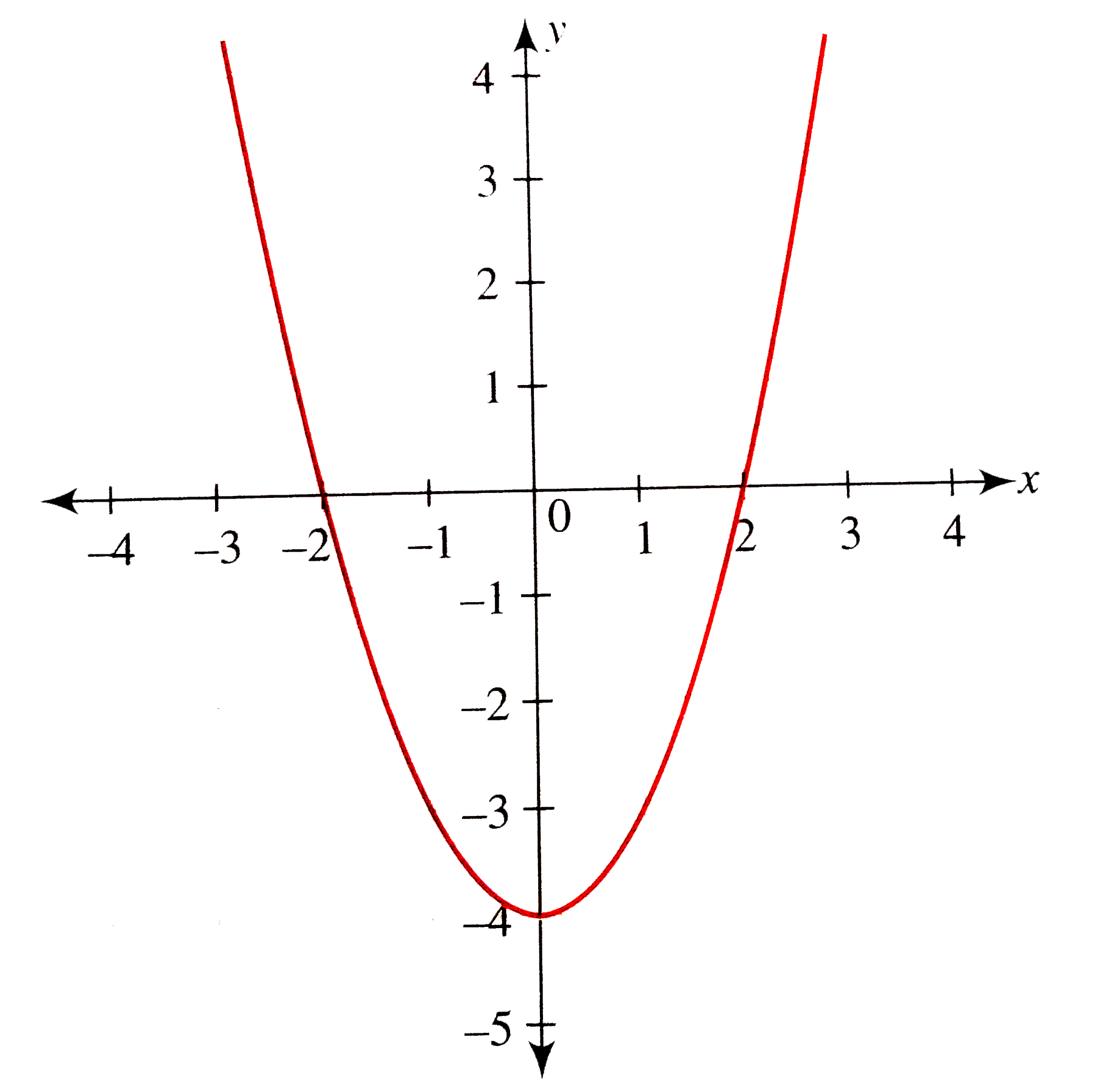



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4
We can find the parabola's equation in vertex form following two steps Step 1 use the (known) coordinates of the vertex, ( h, k), to write the parabola 's equation in the form y = a ( x − h) 2 k the problem now only consists of having to find the value of the coefficient a Step 2 find the value of the coefficient a by substitutingWhen graphing parabolas, find the vertex and yinterceptIf the xintercepts exist, find those as wellAlso, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a Use the leading coefficient, a, to determine if aThe standard x= y2 parabola moves 2 from the vertex and right 4 We expect to go right 4 to the point (0,4) Instead, we went further, to the point (2,4), a distance of 6 The standard is 4, we went 6, so the stretch factor is 6/4 or 3/2 25 The equation of this parabola is x4 = 3 2 (y−2)2 26 To recap The y = x2 parabola points upward, the
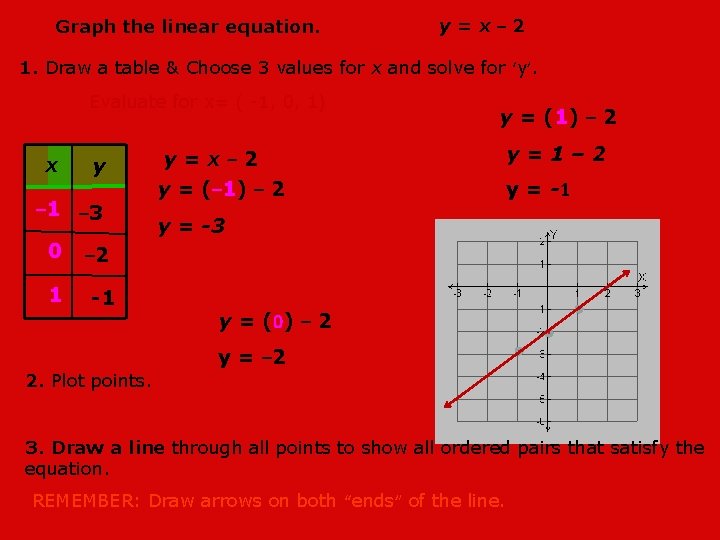



Graph The Linear Equation Yx 2 1 Draw
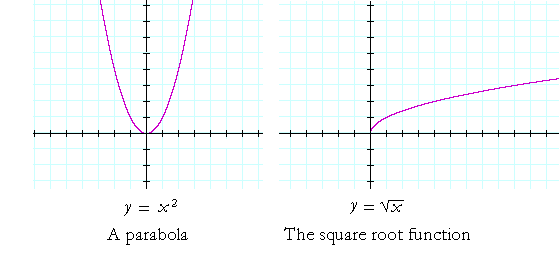



Graph Of A Parabola Topics In Precalculus
Axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=2x^{2} en Related Symbolab blog posts Practice, practice, practice Math can be an intimidating subject Each new topic we learn has symbols and problems we have never seen The unknowingSet y y equal to the new right side y = − x 2 y = x 2 y = − x 2 y = x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens down Opens DownEach parabola is, in some form, a graph of a seconddegree function and has many properties that are worthy of examination Let's begin by looking at the standard form for the equation of a parabola The standard form is (x h) 2 = 4p (y k), where the focus is (h, k p) and



1




Quadratic Systems A Line And A Parabola Video Khan Academy
Y = x 2 3x 13;Parabolas intro Graphs of quadratic functions all have the same shape which we call "parabola" All parabolas have shared characteristics For example, they are all symmetric about a line that passes through their vertex This video covers this and other basic facts about parabolas This is the currently selected item y = x 2, where x ≠ 0 Here are a few quadratic functions y = x 2 5;
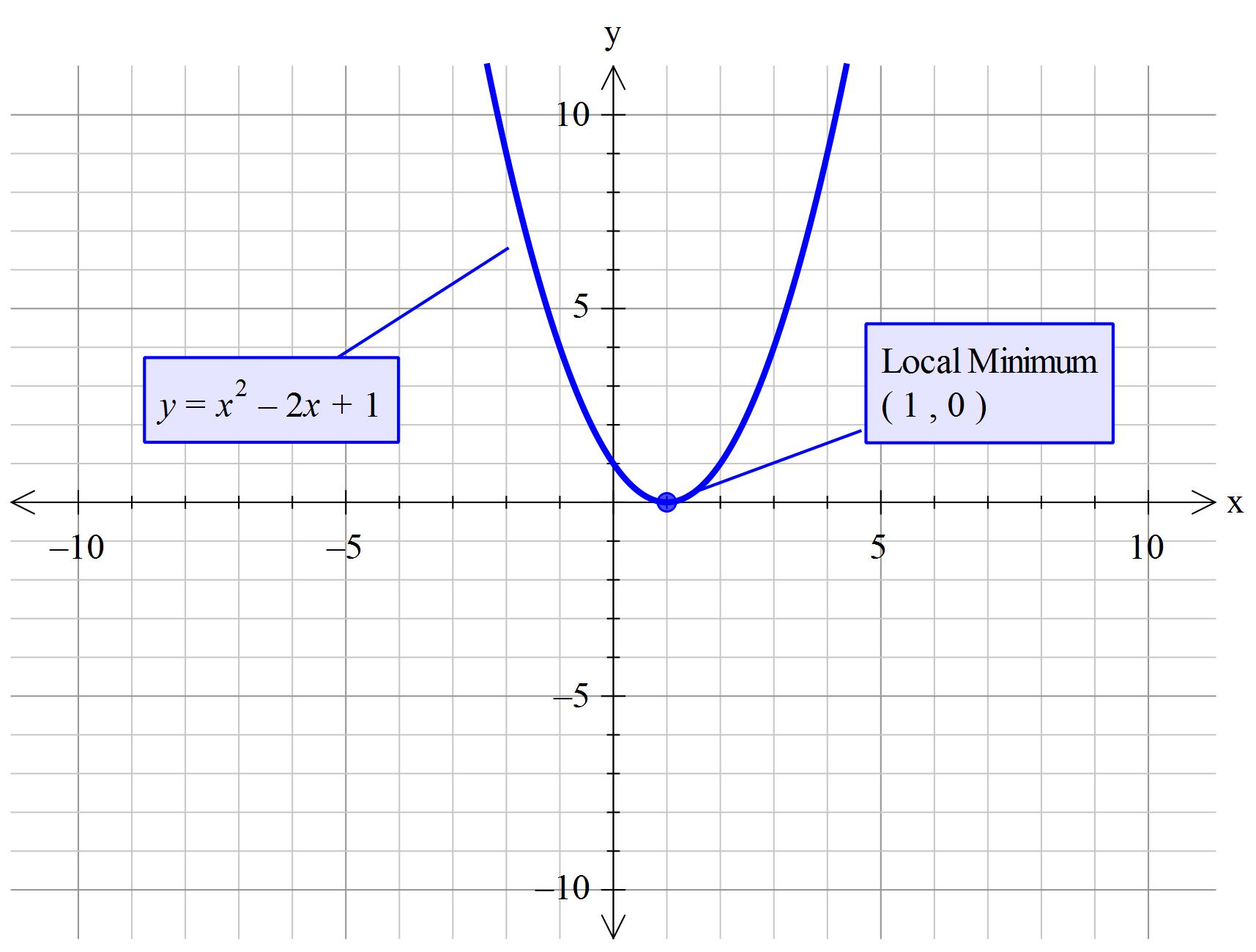



What Is The Vertex Of Y X 2 2x 1 Socratic




Quadratic Function
Below we will see a graph showing how this all looks when full parabolas are drawn Realize that when a = 1 we have our reference parabola y = (1)x 2 = x 2 When a = 1, we have y = (1)x 2 = x 2 When a = 1, all the points on the reference parabola have been reflected over the xaxisThe graph below has the reference parabola drawn in transparent light gray, and it's reflectionThe beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetry Finding the yintercept of a parabola can be tricky Although the yintercept is hidden, it does exist Use the equation of the function to find the yintercept y = 12x 2 48x 49 The yintercept has two parts the xvalue and the yvalue Note that the xvalue is always zero So, plug in zero for x and solve for y
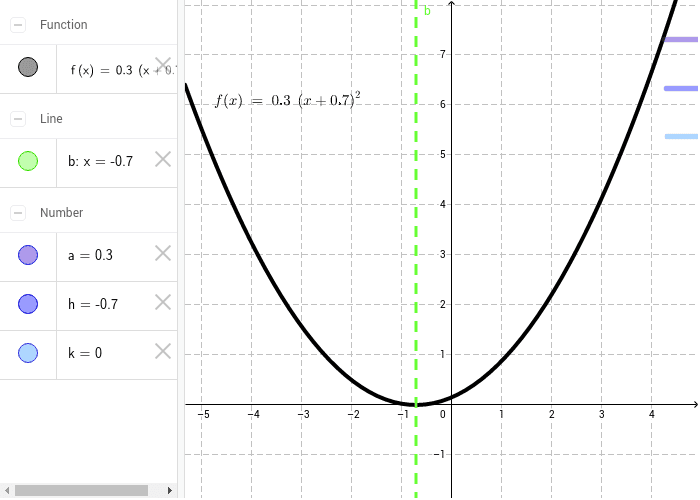



Transformations To The Graph Of Y X 2 Geogebra
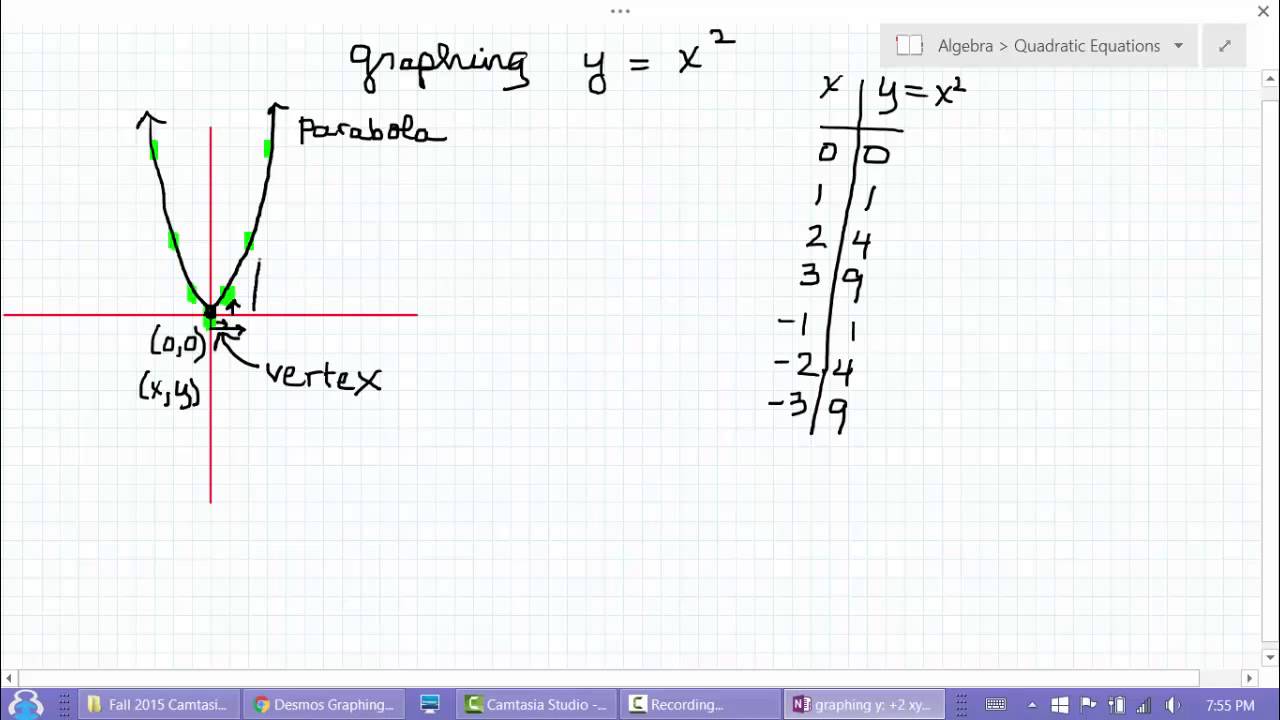



Graphing Basic Parabola Y X 2 Youtube
The Parabola Given a quadratic function f ( x) = a x 2 b x c, it is described by its curve y = a x 2 b x c This type of curve is known as a parabola A typical parabola is shown here Parabola, with equation y = x 2 − 4 x 5Solutions to the Above Questions and Problems Solution The x intercepts are the intersection of the parabola with the x axis which are points on the x axis and therefore their y coordinates are equal to 0 Hence we need to solve the equation 0 = x 2 2 x 3 Factor right side of the equation (x 3) (x 1) () = 0 Before rotating (and plotting), you need to parametrize your parabola { x ( t) = t y ( t) = t 2, where t ∈ R You are rotating each point of the parabola, and hence X ( t) Y ( t) = 2 2 1 − 1 1 1 ⋅ x ( t) y ( t) = 2 2 x ( t) − y ( t) x ( t) y ( t) At the end you get that X ( t) Y ( t) = 2 2




Y X 2
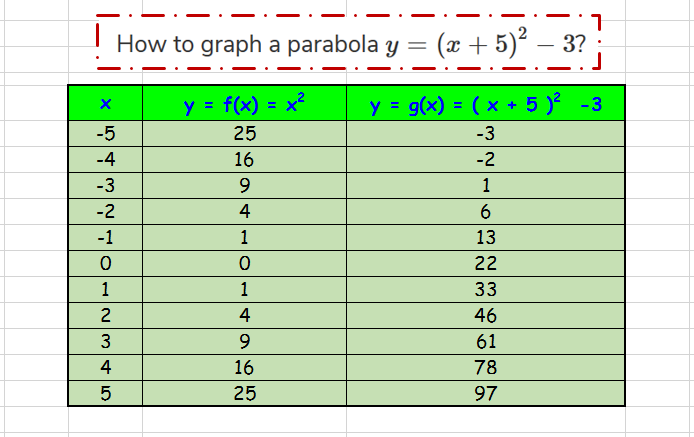



How To Graph A Parabola Y X 5 2 3 Socratic
We're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2, where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0 Let's vary the value of a to determine how the graph changesFor horizontal parabolas, the vertex is x = a(y k) 2 h, where (h,k) is the vertex The focus of parabolas in this form have a focus located at (h , k) and a directrix at x = h The axis of symmetry is located at y = k Vertex form of a parabola The vertex form of a parabola is another form of the quadratic function f(x) = ax 2 bxAnswer to Find the vertex of the following parabola x^2 = 2y By signing up, you'll get thousands of stepbystep solutions to your homework



Graphing Quadratic Functions




Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic
If positive, a hyper



Quadratics Graphing Parabolas Sparknotes




File Parabola Y X 6x 7 Svg Wikimedia Commons



Given The Quadratic Equation Y X 2 6x 5 Find The Vertex Axis Of Symmetry Intercepts Domain Range Interval Where The Function Is Increasing And Enotes Com
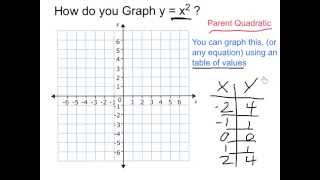



Graph Y X 2 Youtube
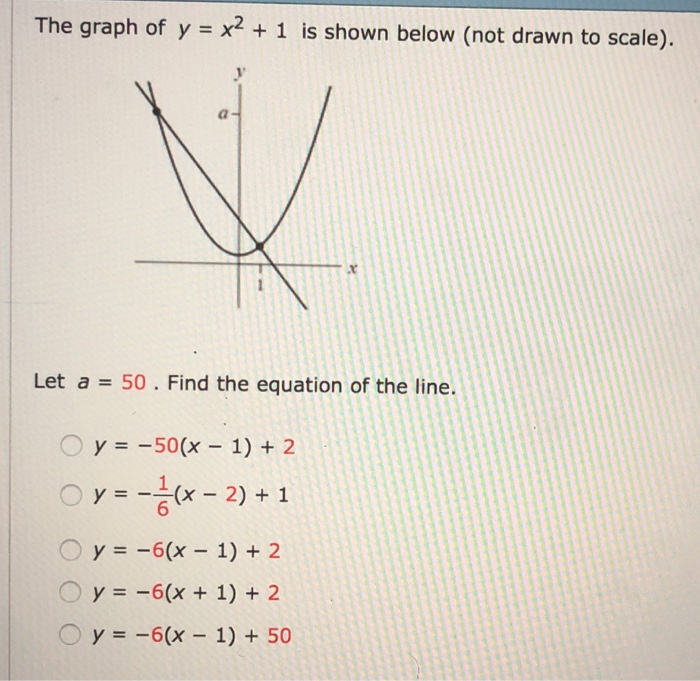



Solved The Graph Of Y X2 1 Is Shown Below Not Drawn To Chegg Com
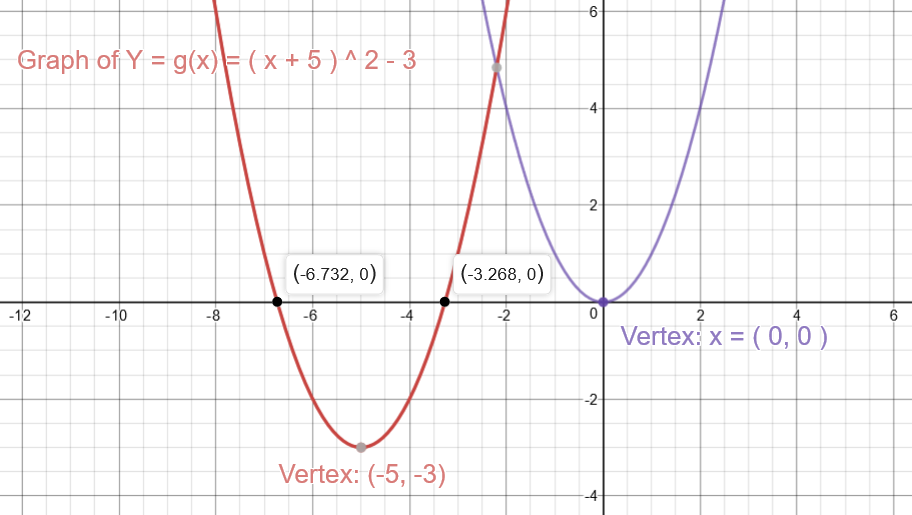



How To Graph A Parabola Y X 5 2 3 Socratic



Parabolas



Y 2x



Where Do Y X 2 4x 1 And Y 3 X Intersect Mathskey Com



Y X 2 2




The Area Enclosed Between The Parabola Y X 2 X 2 And The Line Y X 2 In Sq Unit Is Equal To
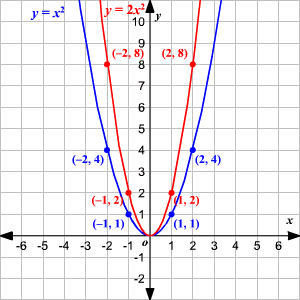



Graphing Quadratic Equations Using Transformations




Graphing Parabolas




Characteristics Of Parabolas College Algebra



What Is The Maximum Vertical Distance Between The Line Math Y X 2 Math And The Parabola Math Y X 2 Math For Math 1 Le X Le 2 Math Quora




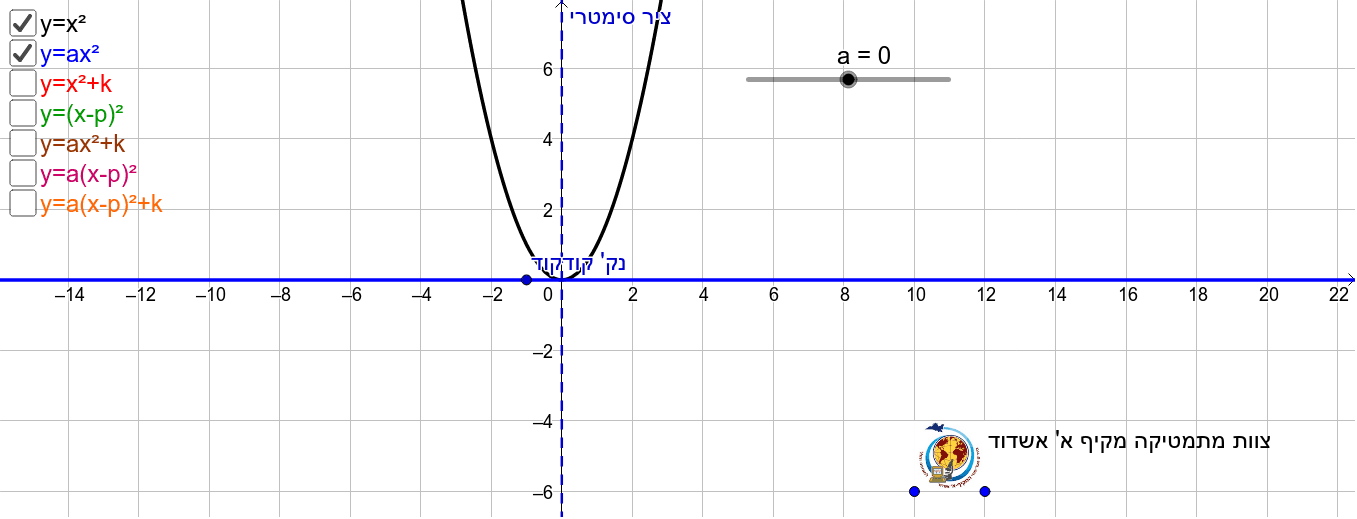
Content Transformations Of The Parabola



Algebra Parabola Transformations Of Y X 2 Graphs Match Up 2 Teaching Resources



Solution Graph Y X 2 1 Label The Vertex And The Axis Of Symmetry And Tell Whether The Parabola Opens Upward Or Downward
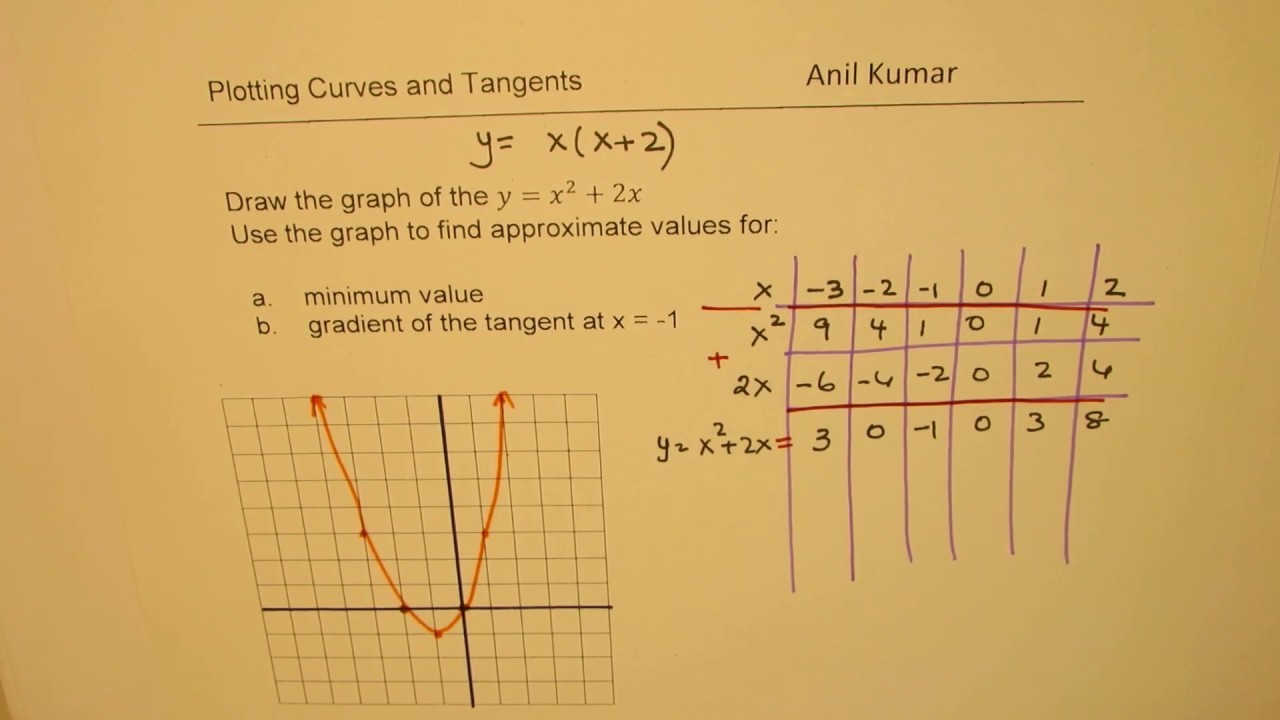



Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube
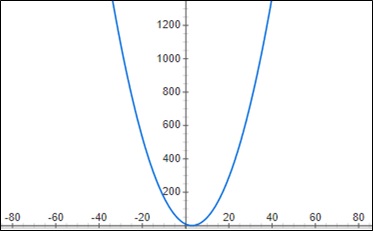



Sketch The Parabola Of Equation Y X 2 6x 9 And Indicate Its Vertex Study Com



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively




Quadratic Function




Three Tangent Lines To The Parabola Y X 2 Corresponding To Three 1d Download Scientific Diagram




How Do You Graph Y X 2 1 Socratic



Y X 2 2



Graph The Parabola Y X 2 6x Mathskey Com



Instructional Unit The Parabola Day 4 And 5




3 2 Quadratic Functions Mathematics Libretexts




Content Transformations Of The Parabola
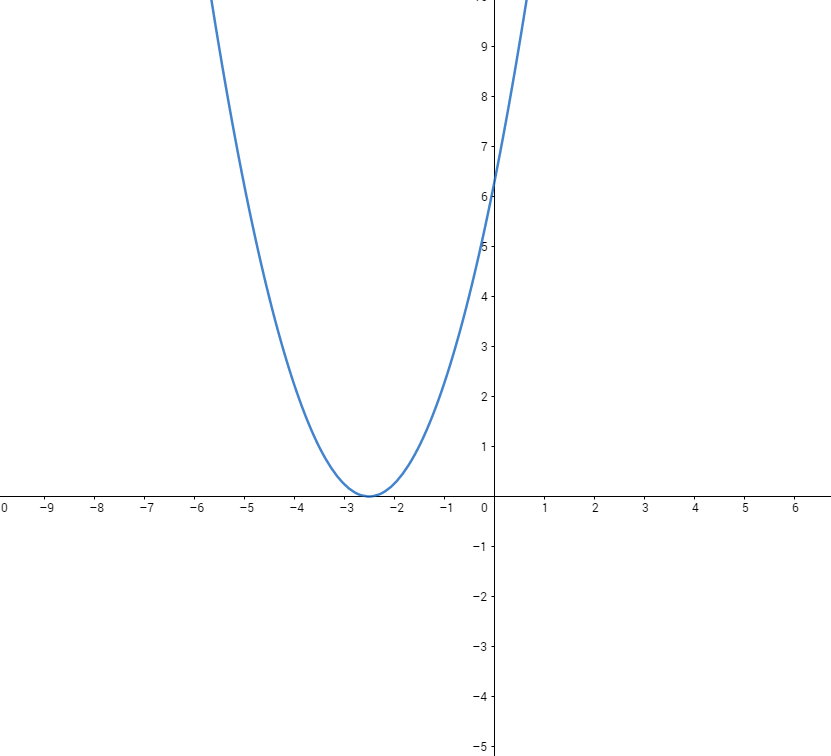



How Do You Graph Y X 2 5x 3 Socratic



We Know How To Graph The Quadratic Equation Y X2




Parabola Parent Function Mathbitsnotebook A1 Ccss Math
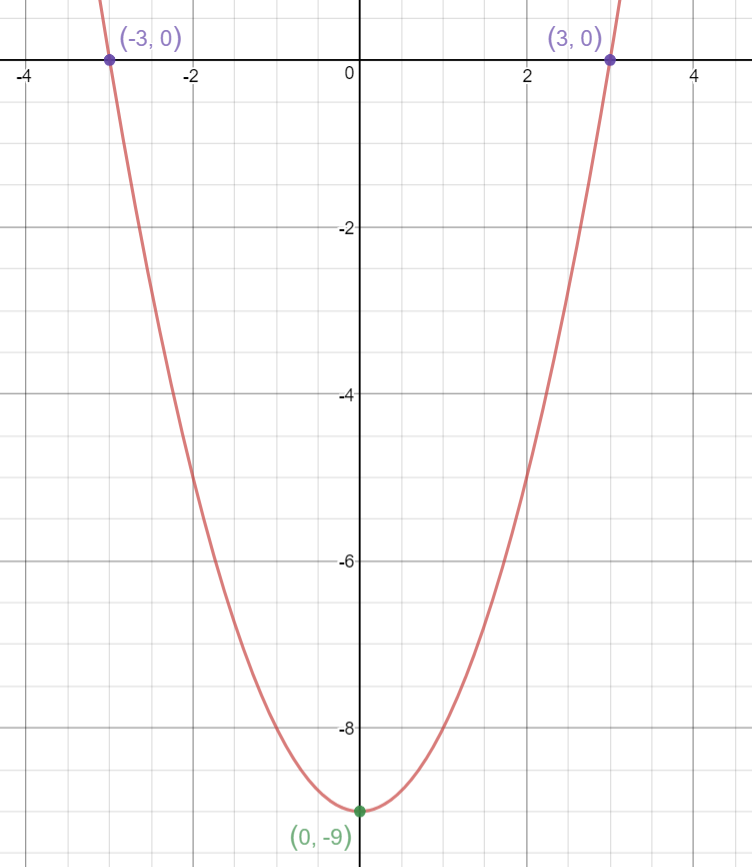



How Do You Graph Y X 2 9 Socratic




The Area Bounded By The Parabola Y 4x 2 Y X 2 9 And The Line Y 2 Is A sqrt2 3 B 10sqrt2 3 C 40sqrt2 3 D Sqrt2 3




Quadratic Function
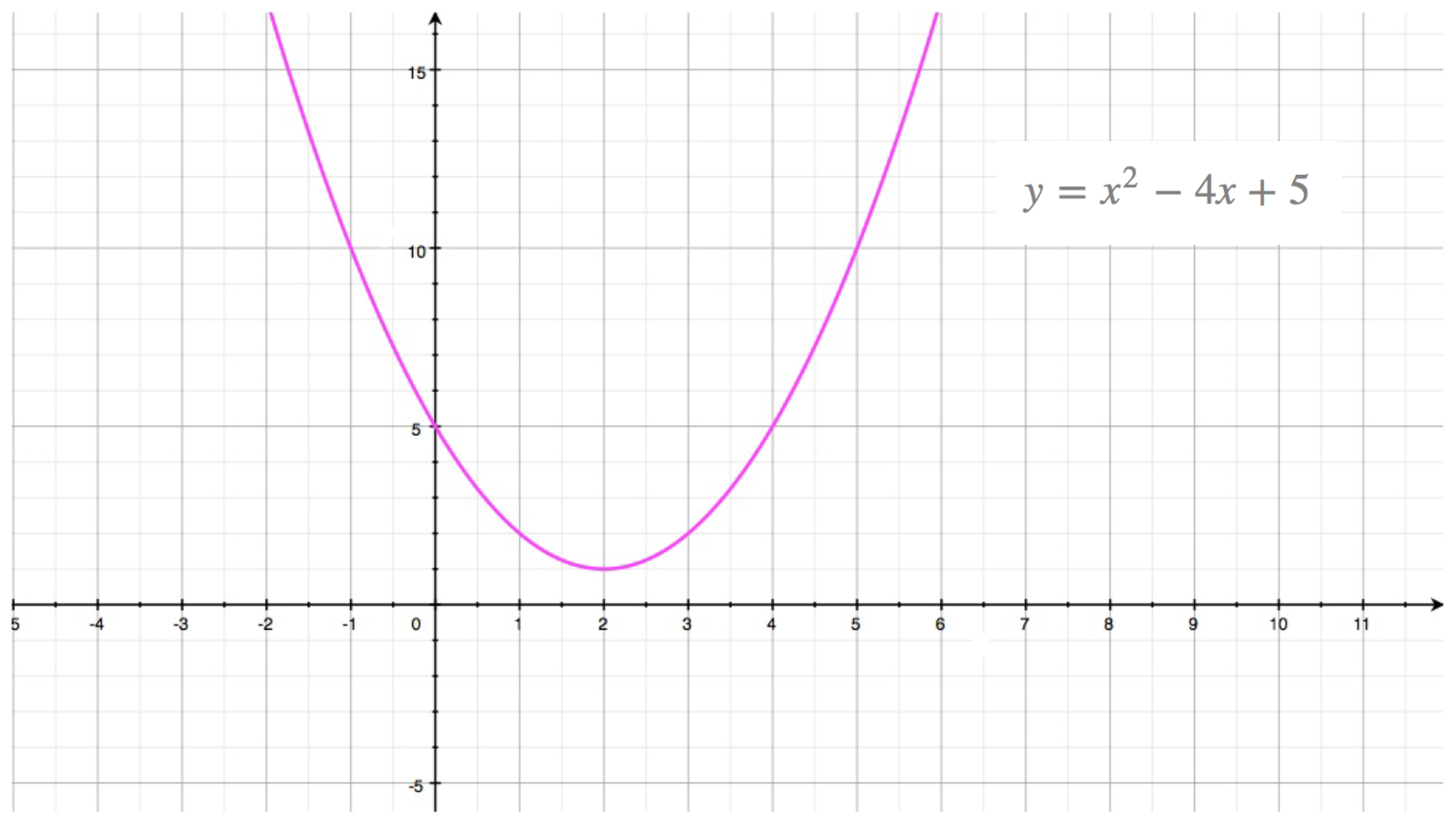



Quadratic Function Parabola




Graphing Parabolas
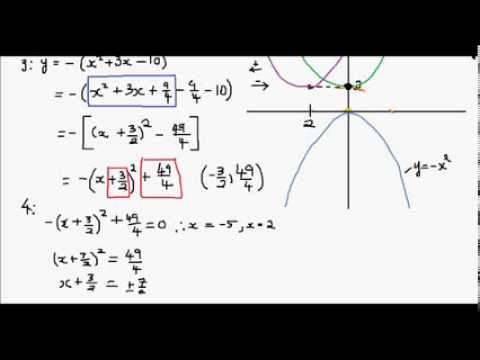



How To Sketch A Parabola Example 1 Y X 2 3x 5 Youtube



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2
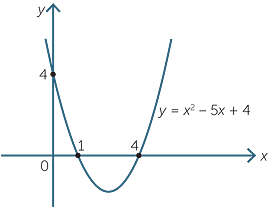



Quadratic Function



Quadratics Graphing Parabolas Sparknotes



Quadratic Graphs Of Y A X B A 0



Parabola Y X 2 Geogebra



Graphing Quadratic Functions
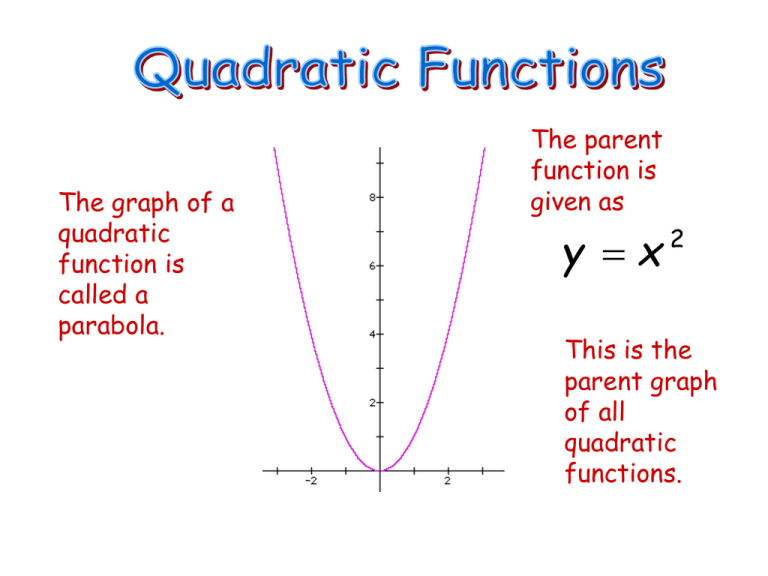



Y X



The Parabola Y X 2 C Is To Be Tangent To The Line X Y What Is The Value Of C Quora




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram




How To Draw Y 2 X 2 Interactive Mathematics




Graph Y X 2 3 Youtube
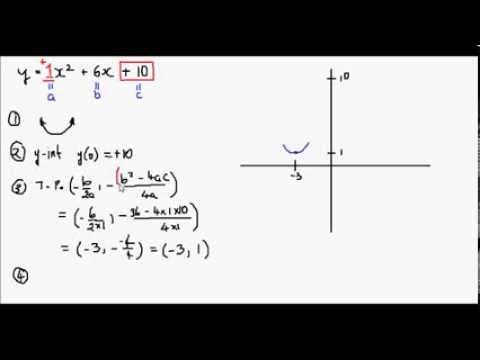



How To Sketch A Parabola Example 3 Y X 2 6x 10 Youtube
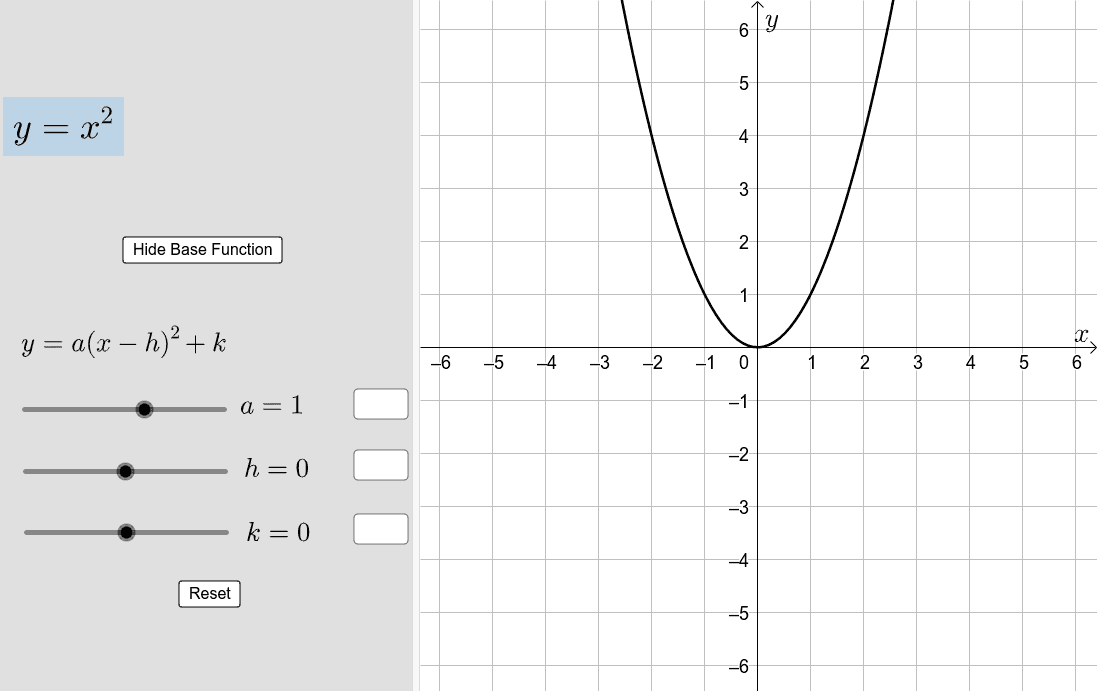



Transforming The Graph Of Y X Geogebra
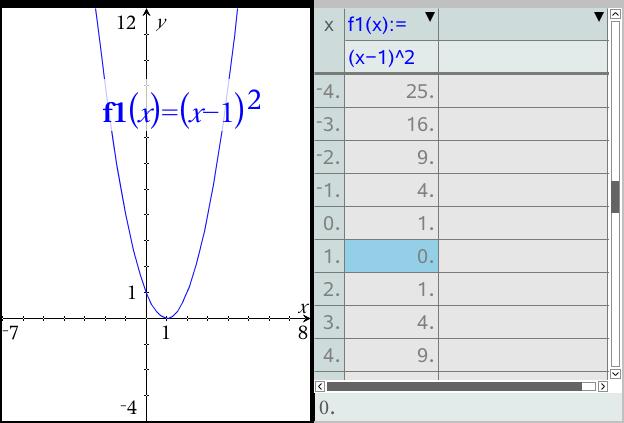



How Do I Graph The Quadratic Equation Y X 1 2 By Plotting Points Socratic



How Do You Sketch The Graph Of Y X 2 2x And Describe The Transformation Socratic




Parabolas Xcelerate Math



Solution Which Parabola Quadratics Underground Mathematics




How To Draw Y 2 X 2 Interactive Mathematics




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
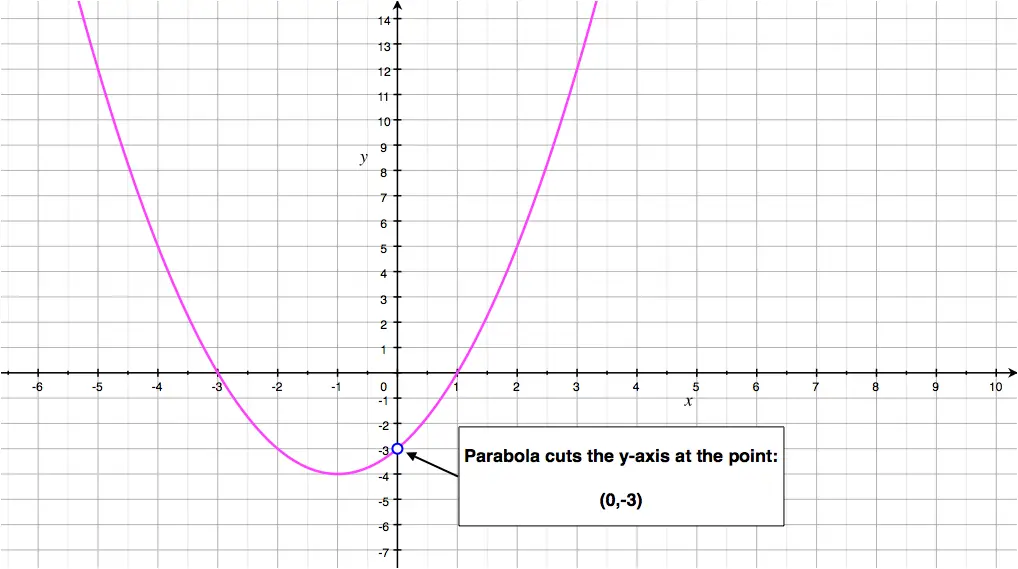



Quadratic Function Parabola




Misc 12 Find Area X Y Y X2 And Y X Class




Graph Y X 2 Study Com




Content Transformations Of The Parabola




How To Draw Y 2 X 2 Interactive Mathematics



Y X 2




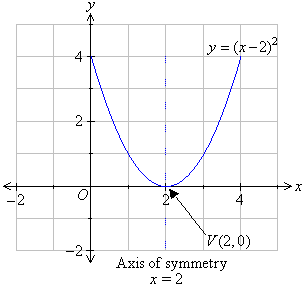
How To Graph A Parabola Of The Form Y X 2 Bx C Algebra Study Com
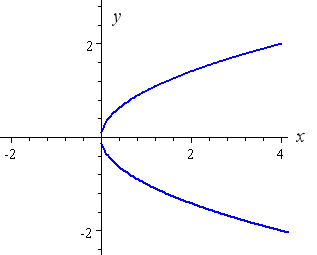



How To Draw Y 2 X 2 Interactive Mathematics



Quadratics Graphing Parabolas Sparknotes



Solution I Do Not Know How To Graph The Parabola Y X 2




Vertical Shifts Of Quadratic Functions Ck 12 Foundation




Graph The Following Equation Y X 2 6x 10 Y X 2 3x 2 Y X 2 6x 10 Y X 2 6x 10 Study Com
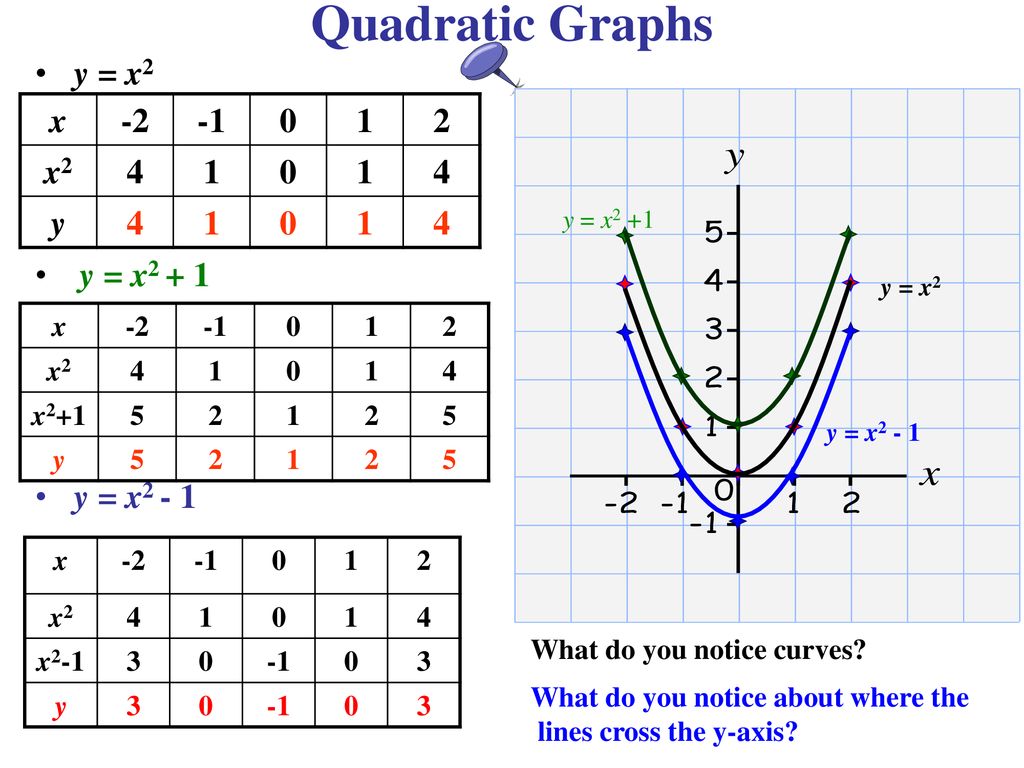



Quadratic Graphs Parabolas Ppt Download
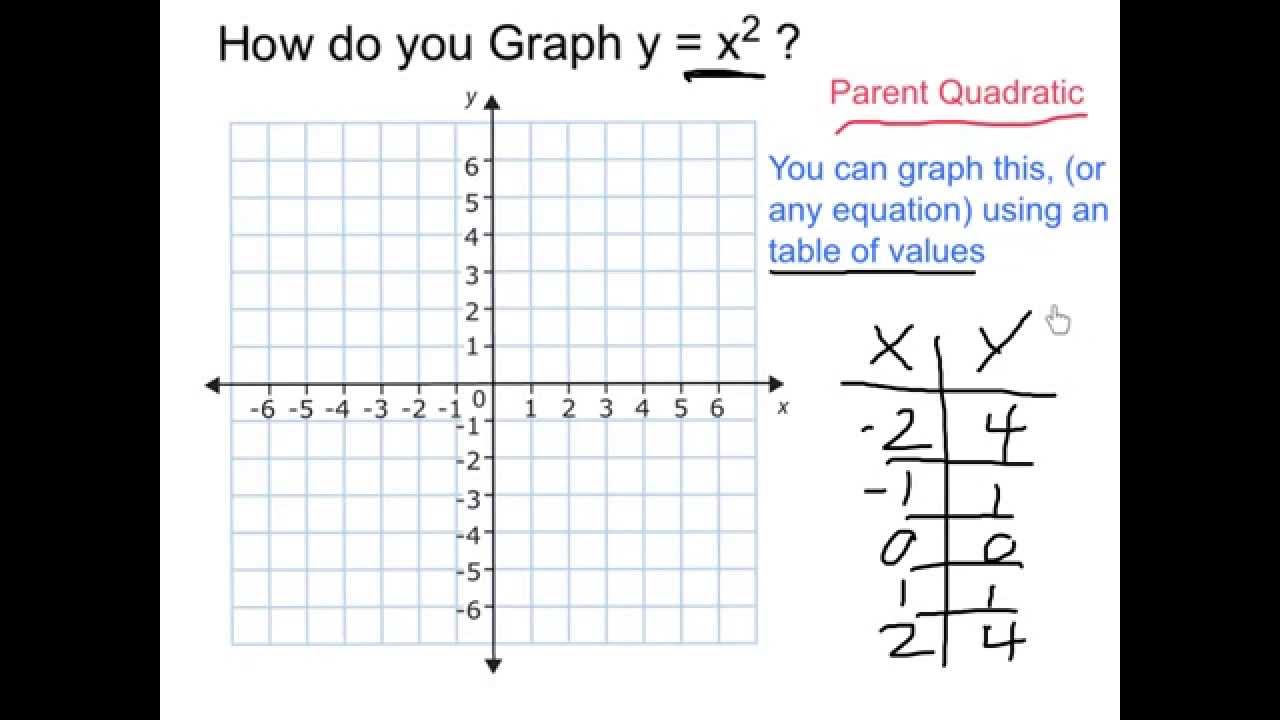



Graph Y X 2 Youtube
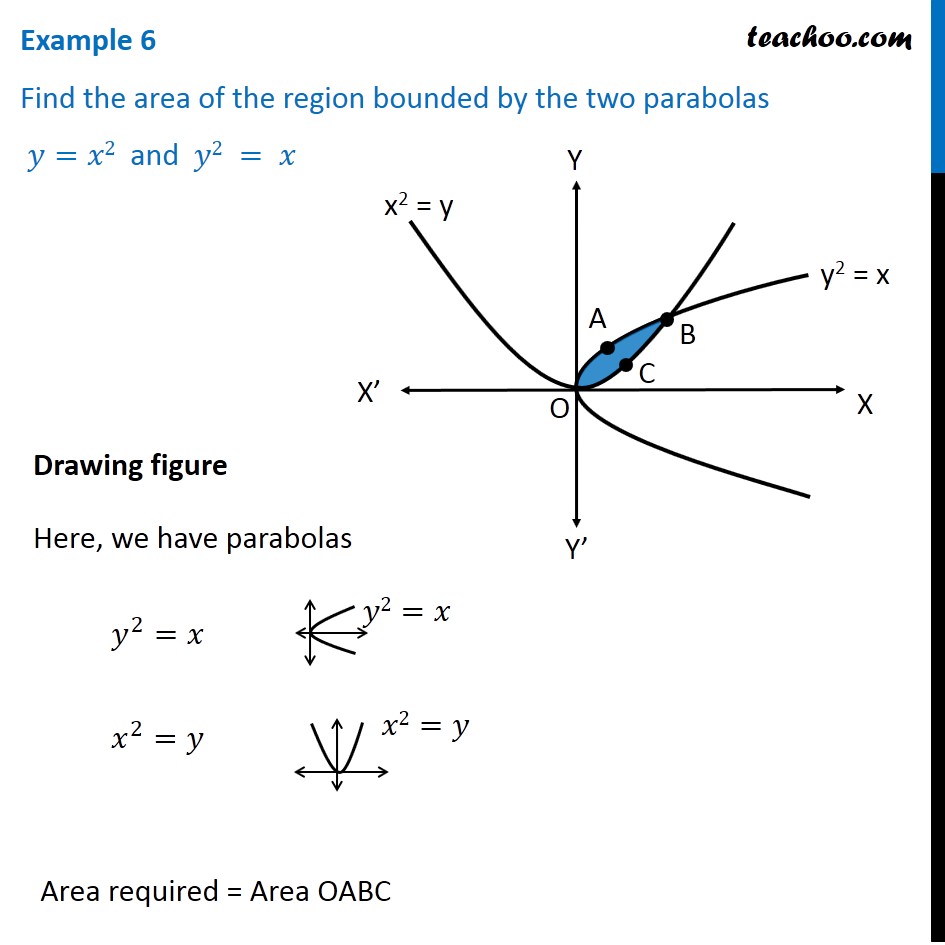



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X




The Graph Of The Quadratic Function Y X2 Is Shown Below If This Parabola Is Reflected About The Brainly Com




Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube




Graphing A Parabola Using Matplotlib In Python Stack Overflow




Transformations Of Quadratic Functions College Algebra




How To Graph Y X 2 1 Youtube




How Do You Graph Y X 2 2x Socratic



0 件のコメント:
コメントを投稿